The Schlogl model was conceived for modeling and simulation of biochemical systems. The Schlogl model depends exclusively on the chemical species X1 with a peculiar features such as bistability and first order phase transition (energy-assisted jumps between states), and front propagation in spatially extended systems (Vellela and Qian 2009). Biochemically, the kinetics accurately capture the dynamics of the system. The set of reactions for the Schlogl reaction network and their corresponding propensities are presented in Table 1. The stochastic reaction rate parameters we employed, which lead to the bistable behavior, are also given in Table 1.

The Schlogl model definition in terms of reactions, propensities and reaction rates (adapted from: S. Ilie et al. 2009).
The model converts species A to B and viceversa via intermediate species X with rate constant given by Table 1. For the deterministic model and the reactions in Table 1 a solution converges to one of the two stable states, and stays in the neighborhood of that solution after a finite time. We can write a deterministic model equation for the rate change of X based on the laws of mass action. The system behaviors can be investigated by exploiting the deterministic approach (Kurtz 1970) which approximates its dynamics through a system of ordinary differential equations (ODEs):
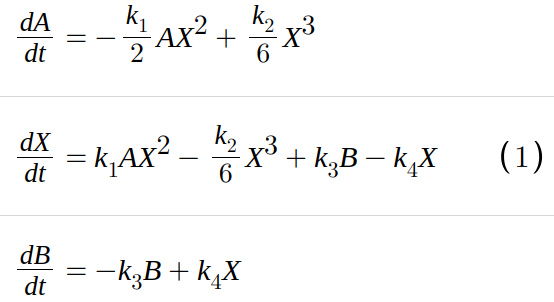
The concentrations of A and B are fixed, and the system is open with the exchange of chemical materials (Cao 2006) If the concentrations of A and B are equal, the system becomes to equilibrium. When the concentration of A and B are fixed, but different, the system shows two stable steady states as solutions for X1. We focus on the single state variable, one-dimensional deterministic bistable Schlogl model, and then to stochastic bistable system.
